Yasushi Narushimanarushima Lab.

Overview of Research

This laboratory focuses on mathematical optimization problems, which appear in various research and application areas, such as engineering and social sciences. Due to the recent emergence of the advanced information society, optimization problems have become increasingly complex. For solving these challenging problems, we investigate mathematical models and numerical algorithms.

Major Taught Courses

Operations Research 4, Mathematics for Industrial and Systems Engineering, Systems Optimization

①Large-scale optimization problems

Due to the recent emergence of the advanced information society, the amount of data that needs to be handled is continuously increasing. Therefore, in recent years, the demand for solve large-scale optimization problems has also considerably increased. However, such large-scale optimization problems cannot always be solved using conventional methods; hence, we are exploring solvable problem formulations and solution algorithms.

• 

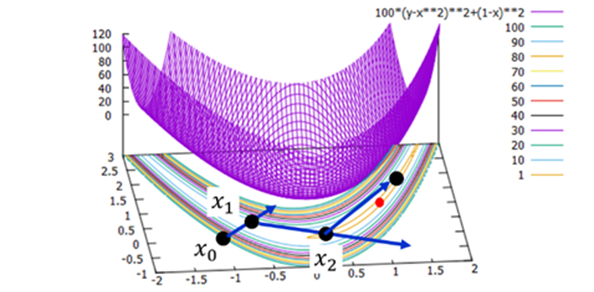
  Image for Mathematical Optimization

②Robust optimization problems

For example, consider an optimization problem that seeks to maximize the sales profit by determining the production volumes of multiple products. In such cases, the unit profits of the products are usually assumed to be constant. However, in reality, they generally change because of various factors, for example, fluctuations in the transportation costs due to soaring gasoline prices. These factors are called uncertainties. We are researching models and methods to find robust solutions to optimization problems subject to uncertainties.

③Equilibrium problems

When there is only one decision maker whose objective is to maximize their profit or minimizes their cost, the resulting problems are referred to as the mathematical optimization problems. On the other hand, when there are multiple decision makers who compete among one another, such problems are called the equilibrium problems. The latter problems are more challenging than ordinary optimization problems. Therefore, we are researching modeling approaches to equilibrium problems and algorithms for solving them.

Recent Research Theme

• Development of algorithms for large-scale optimization problems that occur in machine learning
• Research on equilibrium problems that occur in supply chain networks
• Robust portfolio selection for diversified investment problems

Educational Policies

We can find a suitable solution for real-life mathematical optimization or equilibrium problems only when we have both a suitable model for the problem and an algorithm for solving it. However, as optimization problems have become larger and more complex in recent years, developing new, advanced algorithms has become necessary for solving these problems. Our laboratory aims to educate experts who have the knowledge of both modeling and algorithms and possess advanced skills for solving actual problems.